

Similarly, the larger the moment of inertia of the body, the more difficult it is to stop its rotational motion. For example, if the body is at rest the larger the moment of inertia of the body the more difficult it is to put the body into the rotational motion. In other words, the moment of inertia is the measurement of resistance of the body to a change in its rotational motion. The moment of inertia plays the same role in rotational motion as the mass does in the translational motion. Vedantu provides the complete explanation of the Moment of Inertia in Semicircle for the students of IIT JEE, and that too is free of cost. If you have forgotten the part of the Moment of Inertia in Semicircle, then you do not have to worry at all. And one of the important parts of the system of Particles is that of Moment of Inertia in Semicircle. In which you have learned the motion of the extended body, that is to say, the system of particles. And one of those units is the System of Particles and Rotational motion, which you may have studied in class 11th Physics. And hence, it is very important for the students to study all those units.

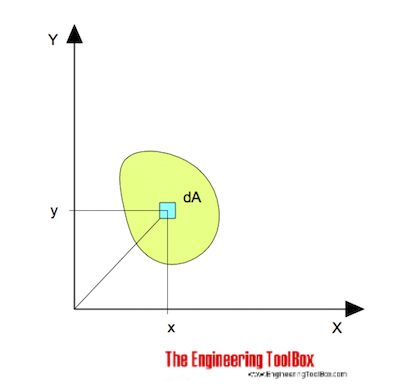
This is the equation of the parallel axis theorem for the second moment of area.The syllabus of the IIT JEE for the subject of Physics covers all the chapters of two previous classes, that is to say, class 11 and class 12. As the first moment of inertia about the centroidal axis is zero, therefore the term `\inty.dA` is equivalent to zero. Thus the term `\inty.dA` indicates the moment of area of the total shape about the centroid itself.

But as shown in the above figure, the distance ‘y’ indicates the position of the area ‘dA’ from the centroid of the object. The term `\inty.dA` indicates the equation for the first moment of area of the shape. Integrate `dI` to find the total mass moment of inertia about axis A-A’. The mass moment of inertia of the smaller mass ‘dm’ about the axis A-A’ is given by,
The axis O-O’ shown in the above figure passes through the center of mass (COM) of the object while the axis A-A’ (parallel to the axis O-O’) is located at a distance ‘h’ from the axis O-O’.Ĭonsider a smaller portion of mass ‘dm’ located at a distance ‘r’ from the center of mass of the object.


 0 kommentar(er)
0 kommentar(er)
